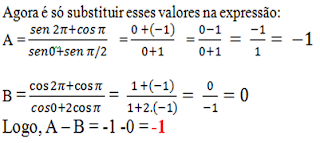RAZÕES TRIGONOMÉTRICAS NA CIRCUNFERÊNCIA - 2º ANO CMA ~ CADERNO DIGITAL

RAZÕES TRIGONOMÉTRICAS NA CIRCUNFERÊNCIA

PROBLEMA 1: O ponteiro maior de um relógio mede aproximadamente 1 m. Em quanto tempo a ponta móvel desse ponteiro percorre em 3π metros?

Solução:

O ponteiro do relógio é equivalente ao raio da circunferência do próprio relógio. Então, a circunferência do relógio mede:

C_{circunferência} = 2πr = 2 . 3,14 . 1 = 6, 28 m

Sabemos que o ponteiro maior do relógio é o ponteiro dos minutos. Logo, ele dá uma volta completa na circunferência em 60 minutos e essa volta completa corresponde ao comprimento total da circunferência que é 6,28m. Assim:

60 min ---------- 6,28m

x min ---------- 3π m

Como 3π = 3 . 3,14 = 9,42m, temos:

60 min ---------6,28m

x min ----------9,42 m

Fazendo o produto dos meios igual ao produto dos extremos, vem:

6,28 x = 60 . 9,42

6,28x = 565,2

x = 565,2/6,28

x = 90 minutos = 1 h 30 min

PROBLEMA 2: Qual o menor ângulo formado pelos ponteiros de um relógio às 16 horas e 15 minutos ?

Solução:

O menor ângulo formado pelos ponteiros de horas e minutos é dado por:

Observe que acima enquanto o ponteiro de minutos dá uma volta completa de 360° o de horas só anda 30°(que é a distância em graus entre uma hora e outra). O ponteiro de minutos anda 90° (distância entre 12 e 3 em graus – lembre-se que pra cada valor no relógio temos 30° , logo: 3.30°= 90°). Então, enquanto o ponteiro de minutos anda 90° o ponteiro de horas andará y. Veja que de 3 para 4 temos 30°.

PROBLEMA 3: Qual o valor numérico da expressão A - B, quando:

Solução:

Primeiro vamos calcular cada um dos valores separadamente:

a) Sen 2π

Pela circunferência trigonométrica podemos observar que o seno de 2π é 0 (não esqueça que seno é referente ao eixo y). O cosseno de π é -1 (não esqueça que cosseno refere-se ao eixo x). O seno de 0 é 0...